指数生成函数
序列
基本运算
指数生成函数的加减法与普通生成函数是相同的,也就是对应项系数相加。
考虑指数生成函数的乘法运算。对于两个序列
因此
的指数生成函数。
封闭形式
我们同样考虑指数生成函数的封闭形式。
序列
因为你将
类似地,等比数列
指数生成函数与普通生成函数
如何理解指数生成函数?我们定义序列
但
这两种理解没有任何问题。也就是说,不同的生成函数只是对问题理解方式的转变。
EGF 中多项式 exp 的组合意义
如果您还没有学习多项式 exp 请先跳过这里,这是由 exp 理解引出的意义,从某种意义上来说可以加深对 EGF 的理解。
EGF 中
对于两个 EGF 相乘得到的
如果
则系数显然为原 EGF 各项常数的积,但是多项式 中某些要求导致 的 常数项必须为 ,具体的原因在下文中会做出一些说明。
多项式系数定义(具体请参考排列组合一栏中的多项式系数组合意义)里是默认集合有序的,但是
设
设
设
对于所有的
上面是从组合角度直接列式理解,我们也可以从递推方面来证明
同样设
上界是由非空集合划分推出的
得到递推式之后可递归展开,边界为
同样的有:
显然 定义成划分为非空集合(
从递推式的角度讲,多个 EGF 的乘积也可以看作一个类似于背包的组合(合并两组计数对象的过程)。
总结多项式
排列与圆排列
长度为
圆排列的定义是把
也就是说
一个排列,是由若干个置换环构成的。例如
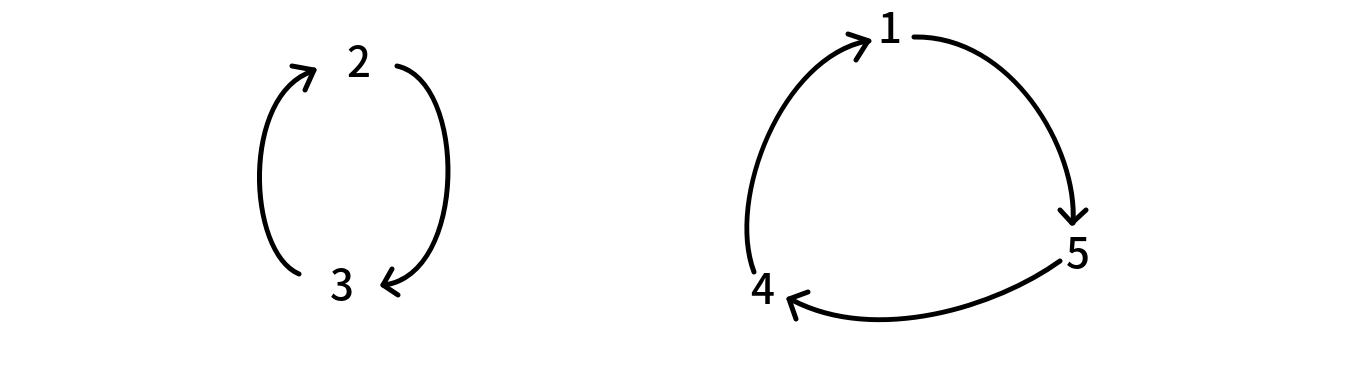
(也就是说我们从
而不同的置换环,会导出不同的排列。例如将第二个置换环改成
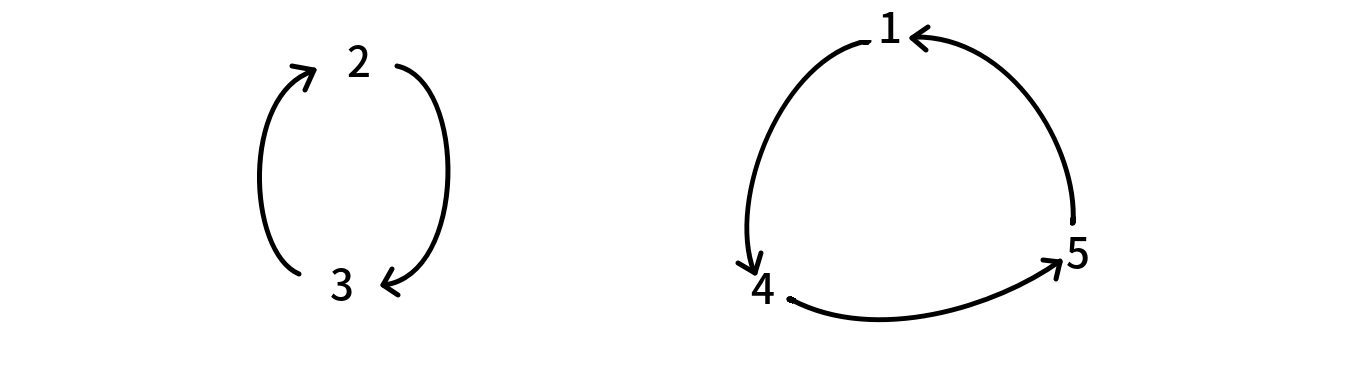
那么它对应的排列就是
也就是说,长度为
- 把
- 每个集合形成一个置换环
的方案数。而一个集合的数形成置换环的方案数显然就是这个集合大小的圆排列方案数。因此长度为
这就是多项式
推广之
- 如果
如果
因此要计算前者,只需要一次多项式
接下来我们来看一些指数生成函数的应用。
应用
错排数
错排数
定义长度为
求错排数的指数生成函数。
从置换环的角度考虑,错排就是指置换环中不存在自环的排列。也就是说不存在长度为
因此错排数的指数生成函数就是
不动点
考虑
考虑
考虑递推求
那么答案的指数生成函数就是
Lust
假设
因此实际上我们的问题转化为,求
不妨考虑计算每种方案的的
而
这与指数生成函数乘法的系数类似。
设
那么答案就是
为了快速计算答案,我们需要将
因此我们得到
其中
计算这个多项式的
本页面最近更新:2023/9/1 16:49:46,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:sshwy, ComeIntoCalm, countercurrent-time, Early0v0, Enter-tainer, GhostLX-AI, Great-designer, NachtgeistW, shuzhouliu, SukkaW, Tiphereth-A, untitledunrevised
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用