Stern–Brocot 树与 Farey 序列 连分数的树 有两种主要方法,可以将所有可能的连分数,合并为有用的树结构。
Stern–Brocot 树 定义 Stern–Brocot 树是一种维护分数的优雅的结构,包含所有不同的正有理数。这个结构由 Moritz Stern 在 1858 年和 Achille Brocot 在 1861 年发现。
解释 Stern–Borcot 树从两个简单的分数开始:
这个
每次在相邻的两个分数
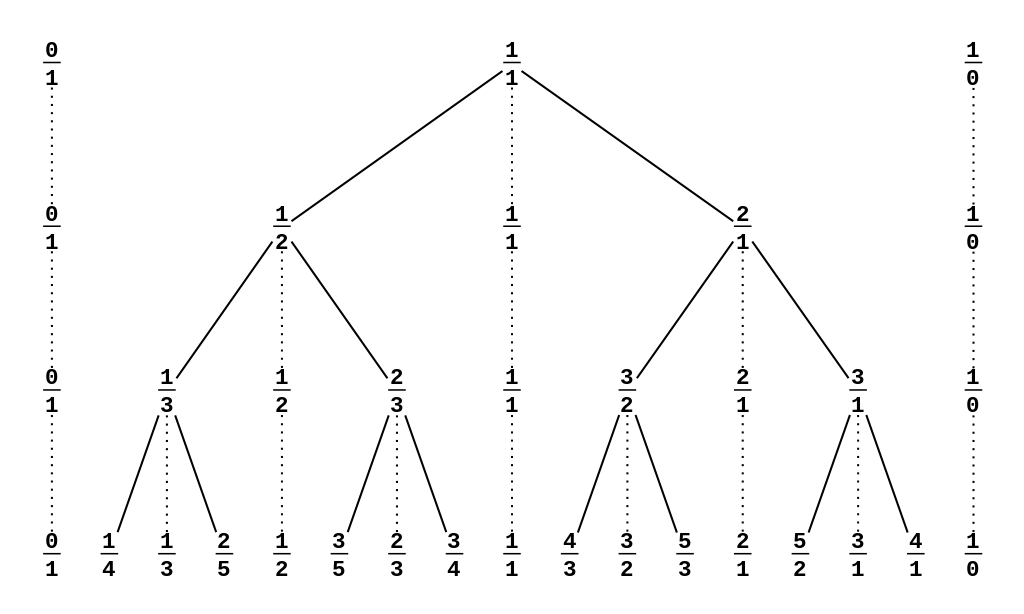
既然称它为 Stern–Brocot 树,那么它总得有一个树的样子。来一张图:
可以把第
性质 接下来讨论 Stern–Brocot 树的性质。
单调性 在每一层的序列中,真分数是单调递增的。
略证:只需要在
就行了。这个很容易,直接做一下代数变换即可
另一边同理可证。
最简性 序列中的分数(除了
略证:为证明最简性,我们首先证明对于序列中连续的两个分数
显然,只需要在
后半部分同理。证明了这个,利用扩展欧几里德定理,如果上述方程有解,显然
有了上面的证明,可以证明
有了这两个性质,就可以把它当成一棵平衡树来做了。建立和查询就向平衡树一样做就行了。
连分数表示与父子节点 递推
连分数节点
换句话说,当
因此,
索引 为 Stern Brocot 树编制索引。根顶点被分配了一个索引
在这种索引中,连分数表示规定了有理数的 游程长度编码 (run-length encoding)。
对于
另一个例子是
值得注意的是,Stern–Brocot 树实际上是一个堆。也就是说,它是
实现 构建实现
C++ Python
void build ( int a = 0 , int b = 1 , int c = 1 , int d = 0 , int level = 1 ) {
int x = a + c , y = b + d ;
// ... output the current fraction x/y
// at the current level in the tree
build ( a , b , x , y , level + 1 );
build ( x , y , c , d , level + 1 );
}
def build ( a = 1 , b = 1 , c = 1 , d = 0 , level = 1 ):
x = a + c
y = b + d
# ... output the current fraction x/y
# at the current level in the tree
build ( a , b , x , y , level + 1 )
build ( x , y , c , d , level + 1 )
查询实现
C++ Python
string find ( int x , int y , int a = 0 , int b = 1 , int c = 1 , int d = 0 ) {
int m = a + c , n = b + d ;
if ( x == m && y == n ) return "" ;
if ( x * n < y * m )
return 'L' + find ( x , y , a , b , m , n );
else
return 'R' + find ( x , y , m , n , c , d );
}
def find ( x , y , a = 0 , b = 1 , c = 1 , d = 0 ):
m = a + c
n = b + d
if x == m and y == n :
return ""
if x * n < y * m :
return "L" + find ( x , y , a , b , m , n )
else :
return "R" + find ( x , y , m , n , c , d )
例题 比较连分数的大小 对于
解答 假设
正如已经提到的,在这个表示中,
换言之,对于无理数
现在,正式使用
哪一个对应于
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 # check if a < b assuming that a[-1] = b[-1] = infty and a != b
def less(a, b):
a = [(-1)**i*a[i] for i in range(len(a))]
b = [(-1)**i*b[i] for i in range(len(b))]
return a < b
# [a0; a1, ..., ak] -> [a0, a1, ..., ak-1, 1]
def expand(a):
if a: # empty a = inf
a[-1] -= 1
a.append(1)
return a
# return a-eps, a+eps
def pm_eps(a):
b = expand(a.copy())
a.append(float('inf'))
b.append(float('inf'))
return (a, b) if less(a, b) else (b, a)
最佳内点 对于
解答 就 Stern–Brocot 树而言,这意味着需要找到
因此,如果
对于有理数
1
2
3
4
5
6
7
8
9
10
11
12
13 # finds lexicographically smallest (q, p)
# such that p0/q0 < p/q < p1/q1
def middle(p0, q0, p1, q1):
a0 = pm_eps(fraction(p0, q0))[1]
a1 = pm_eps(fraction(p1, q1))[0]
a = []
for i in range(min(len(a0), len(a1))):
a.append(min(a0[i], a1[i]))
if a0[i] != a1[i]:
break
a[-1] += 1
p, q = convergents(a)
return p[-1], q[-1]
GCJ 2019, Round 2 - New Elements: Part 2 您得到
在这类配对中,找到词典中最小的一对。
解答 重新表述语句,
在这些方程中,对于
让
现在的问题是,给定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 def solve():
n = int(input())
C = [0] * n
J = [0] * n
# p0/q0 < y/x < p1/q1
p0, q0 = 0, 1
p1, q1 = 1, 0
fail = False
for i in range(n):
C[i], J[i] = map(int, input().split())
if i > 0:
A = C[i] - C[i - 1]
B = J[i] - J[i - 1]
if A <= 0 and B <= 0:
fail = True
elif B > 0 and A < 0: # y/x > (-A)/B if B > 0
if (-A) * q0 > p0 * B:
p0, q0 = -A, B
elif B < 0 and A > 0: # y/x < A/(-B) if B < 0
if A * q1 < p1 * (-B):
p1, q1 = A, -B
if p0 * q1 >= p1 * q0 or fail:
return "IMPOSSIBLE"
p, q = middle(p0, q0, p1, q1)
return str(q) + " " + str(p)
Calkin–Wilf 树 定义 在二叉树中组织连分数的一种更简单的方法是 Calkin–Wilf 树。
通常如下所示:
树的根节点为
性质 与 Stern–Brocot 树不同,Calkin–Wilf 树不是二叉搜索树,因此不能用于执行有理二叉搜索。
在 Calkin–Wilf 树中,当
在 Stern–Brocot 树中使用了收敛的递归。为了得出连分数和 Calkin–Wilf 树之间的联系,应该使用完整商(complete quotients)的递归。如果
另一方面,当
当 当 当 相应地,
值得注意的是,如果以广度优先搜索顺序枚举 Calkin–Wilf 树的顶点(即,根有一个数字
因此,Stern–Brocot 树和 Calkin–Wilf 树的相同级别上的数字是相同的,但它们的排序通过 位反转排列 (bit-reversal permutation)而不同。
Farey 序列 定义 Stern–Brocot 树与 Farey 序列有着极其相似的特征。第
显然,上述构建 Stern–Brocot 树的算法同样适用于构建 Farey 序列。因为 Stern–Brocot 树中的数是最简分数,因此在边界条件(分母)稍微修改一下就可以形成构造 Farey 序列的代码。可以认为 Farey 序列
Farey 序列同样满足最简性和单调性,并且满足一个与 Stern–Brocot 树相似的性质:对于序列中连续的三个数
由 Farey 序列的定义,可以得到
中间分数 对于
中间分数还包含这样的分数:
这些中间分数介于
对于给定的
对比上述表达式与
可以得到
两个相邻中间分数的差为
对于确定的
定理:对实数
证明 一种证法可以定量计算。根据连分数中的定理有
由于
因此
取倒数即证毕。
另一种证法使用中间分数。首先,两个相邻渐进分数之间的距离有
由于
对于不等式左边,由于对于固定的
因此有距离关系
更换下标,不等式左边即证毕。
在使用中这个定理经常放缩一下。由于
右半部分
Dirichlet 逼近定理 Dirichlet 逼近定理是说,对于任意的一个无理数
由于任一实数
Dirichlet 逼近定理将右侧优化到了
当
另外还有瓦伦定理:实数
另外还有伯雷尔定理:实数
这个
另外还有定理:实数
其他的,还有 Kronecker 逼近定理:
如果
Dirichlet 逼近定理和 Kronecker 逼近定理,都可以用抽屉原理来解决。事实上,正是 Dirichlet 为了解决 Pell 方程 ,研究有理数逼近条件,抽屉原理才在历史上被第一次正式提出。
当然,采用抽屉原理的证明可以发现,下文中提到的最佳逼近有理数列,每项满足定理中右边改成分母为一次式的不等式。
进一步有结论,渐进有理数列中,每一项均满足 Dirichlet 逼近定理的不等式。
最佳有理逼近 讨论如何用有理数「最佳地」逼近无理数,不妨假设无理数落入
「最佳」一词的概念:选定的有理数必须保证,比它与无理数的距离更近的有理数,分母都比它大。不存在分母比它小的有理数,到给定无理数的距离更近。
最佳有理数:在 Farey 数列的某一行中,与给定无理数距离最近的那个有理数。
这个有理数可能在下面几行依旧与无理数「距离最近」,但一定有某一行,会找到一个新的有理数,与无理数距离更近。因此去重复后可以得到 最佳逼近有理数列 ,分母严格递增,距离递减。
更加严谨的叙述为:
对实数
则称
比无理数大的称为上逼近,否则为下逼近。由于无理数和有理数之间一定有有理数,最佳逼近有理数列必然为若干个上逼近,之后若干个下逼近,交替进行的形式。
有结论:
渐进分数必然为最佳有理逼近。
偶项渐进分数全都是下逼近,奇项渐进分数全都是上逼近。渐进分数列是下上交错的逼近。
在最佳逼近有理数列中,渐进分数是下上关系改变之前的倒数第一个数。如果将最佳逼近有理数列都写成有限简单连分数,那么在渐进分数之后(下上关系改变之后),连分数长度加一。
例如,
那么它的渐进分数列是:
它的最佳逼近有理数列是:
从每个渐进分数(不包含)开始,到下一个渐进分数(包含)为止,同为上逼近,或同为下逼近。
在最佳逼近列中,每一个最佳分数是上一个最佳分数与再往前一个渐进分数的分子分母对应求和。
性质 定理:最佳有理逼近一定是中间分数。
它的逆定理并不成立,中间分数不一定是最佳有理逼近。
证明 首先,
当然,除非
当
因为中间分数可以任意接近
于是有
另一方面,
因此有
分母更小的分数
渐进分数的等价性质 实数
对于任意的整数
也就是
根据等价性,这可以直接作为渐进分数的另一个定义方法。这个性质比最佳逼近更加严格,因此根据这个性质,渐进分数必然为最佳逼近。
证明:
首先有
于是有
即
接下来证明,满足这个条件的都是渐进分数。
首先,越高阶的渐近分数越靠近
这是因为
整理即为上式。
接下来找出分母为
在给定
当
这里的
从上述选取方式可以看出
又根据严格单调性,在
至此距离证毕只剩下
如果给定
如果它们不互素,记
使得
此时将有理数
由于
此时有更小的
勒让德判别法 对实数
则
勒让德判别法的原始形式更加复杂,由勒让德(Legendre)于 1797 年发表在他的专著中。
勒让德判别法的原始表述是一个等价关系,这里给出的形式相对简化与宽松,是一个渐进分数的充分条件而非必要条件。
证明 假设
于是有
此时首先两个分数之间的距离有
又有绝对值不等式
连起来有
整理有
本页面主要译自博文 Дерево Штерна-Броко. Ряд Фарея 与其英文翻译版 The Stern-Brocot Tree and Farey Sequences 。其中俄文版版权协议为 Public Domain + Leave a Link;英文版版权协议为 CC-BY-SA 4.0。
2024/5/8 20:33:33 ,更新历史 在 GitHub 上编辑此页! iamtwz , StudyingFather , 1804040636 , c8ef , CCXXXI , CookiePieWw , countercurrent-time , diauweb , dkz051 , Enter-tainer , Great-designer , H-J-Granger , Ir1d , jiang1997 , LLLMMKK , lyccrius , Menci , NachtgeistW , shawlleyw , shuzhouliu , sshwy , SukkaW , TianKong-y , Tiphereth-A , untitledunrevised , Xeonacid , yanboishere , yusancky CC BY-SA 4.0 和 SATA