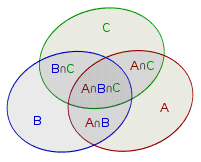
容斥原理 引入 入门例题 假设班里有
是
为了叙述方便,我们把喜欢语文、数学、编程的学生集合分别用
把上述问题推广到一般情况,就是我们熟知的容斥原理。
定义 设 U 中元素有 n 种不同的属性,而第 i 种属性称为
即
证明 对于每个元素使用二项式定理计算其出现的次数。对于元素 x,假设它出现在
于是每个元素出现的次数为 1,那么合并起来就是并集。证毕。
补集 对于全集 U 下的 集合的并 可以使用容斥原理计算,而集合的交则用全集减去 补集的并集 求得:
右边使用容斥即可。
可能接触过容斥的读者都清楚上述内容,而更关心的是容斥的应用。
那么接下来我们给出 3 个层次不同的例题来为大家展示容斥原理的应用。
不定方程非负整数解计数 不定方程非负整数解计数 给出不定方程
没有限制时 如果没有
略证:插板法。
相当于你有
于是我们再加入
容斥模型 接着我们尝试抽象出容斥原理的模型:
全集 U:不定方程 元素:变量 属性: 目标:所有变量满足对应属性时集合的大小,即
这个东西可以用
那么问题变成,对于一些 下界限制 ,而有些则没有限制。
能否消除这些下界限制呢?既然要求的是非负整数解,而有些变量的下界又大于 把这个下界减掉 ,就可以使得这些变量的下界变成
的不定方程形式为
于是这个也可以组合数计算啦。这个长度为
HAOI2008 硬币购物 HAOI2008 硬币购物 4 种面值的硬币,第 i 种的面值是
如果用背包做的话复杂度是
采用同样的容斥方式,
也就是无限背包问题。这个问题可以预处理,算上询问,总复杂度
代码实现 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 #include <bits/stdc++.h>
using namespace std ;
const long long S = 1e5 + 5 ;
long long c [ 5 ], d [ 5 ], n , s ;
long long f [ S ];
int main () {
scanf ( "%lld%lld%lld%lld%lld" , & c [ 1 ], & c [ 2 ], & c [ 3 ], & c [ 4 ], & n );
f [ 0 ] = 1 ;
for ( long long j = 1 ; j <= 4 ; j ++ )
for ( long long i = 1 ; i < S ; i ++ )
if ( i >= c [ j ]) f [ i ] += f [ i - c [ j ]]; // f[i]:价格为i时的硬币组成方法数
for ( long long k = 1 ; k <= n ; k ++ ) {
scanf ( "%lld%lld%lld%lld%lld" , & d [ 1 ], & d [ 2 ], & d [ 3 ], & d [ 4 ], & s );
long long ans = 0 ;
for ( long long i = 1 ; i < 16 ;
i ++ ) { // 容斥,因为物品一共有4种,所以从1到2^4-1=15循环
long long m = s , bit = 0 ;
for ( long long j = 1 ; j <= 4 ; j ++ ) {
if (( i >> ( j - 1 )) % 2 == 1 ) {
m -= ( d [ j ] + 1 ) * c [ j ];
bit ++ ;
}
}
if ( m >= 0 ) ans += ( bit % 2 * 2 - 1 ) * f [ m ];
}
printf ( "%lld \n " , f [ s ] - ans );
}
return 0 ;
}
完全图子图染色问题 前面的三道题都是容斥原理的正向运用,这道题则需要用到容斥原理逆向分析。
完全图子图染色问题 A 和 B 喜欢对图(不一定连通)进行染色,而他们的规则是,相邻的结点必须染同一种颜色。今天 A 和 B 玩游戏,对于 完全图
数学形式 一看这道题的算法趋向并不明显,因此对于棘手的题目首先抽象出数学形式。得分差即为奇偶对称差,可以用 -1 的幂次来作为系数。我们求的是
容斥模型 相邻结点染同一种颜色,我们把它当作属性。在这里我们先不遵守染色的规则,假定我们用 m 种颜色直接对图染色。对于图 元素 。属性
而属性 集合 定义为
回到题目,「相邻的结点必须染同一种颜色」,可以理解为若干个
上述式子右边的含义就是说对于 S 内的每一条边
是不是很有容斥的味道了?由于容斥原理本身没有二元组的形式,因此我们把 所有 的边
同时 S 可以表示为若干个 k 组成的集合,即
而 E 对应集合
逆向分析 那么要求的式子展开
于是就出现了容斥原理的展开形式,因此对这个式子逆向推导
再考虑等式右边的含义,只要满足
解决这道题,我们首先抽象出题目数学形式,然后从题目中信息量最大的条件,逆向推导 出最终的结果。这道题体现的正是容斥原理的逆用。
数论中的容斥 使用容斥原理能够巧妙地求解一些数论问题。
容斥原理求最大公约数为 k 的数对个数 考虑下面的问题:
求最大公约数为 设
这道题固然可以用欧拉函数或莫比乌斯反演的方法来做,但是都不如用容斥原理来的简单。
由容斥原理可以得知,先找到所有以 公约数 的数对,再从中剔除所有以 公约数 的数对,余下的数对就是以 最大公约数 的数对。即 公约数 的数对个数 公约数 的数对个数。
进一步可发现,以 公约数 的数对个数等于所有以 最大公约数 的数对个数之和。于是,可以写出如下表达式:
由于当
for ( long long k = N ; k >= 1 ; k -- ) {
f [ k ] = ( N / k ) * ( N / k );
for ( long long i = k + k ; i <= N ; i += k ) f [ k ] -= f [ i ];
}
上述方法的时间复杂度为
附赠三倍经验供大家练手。
容斥原理推导欧拉函数 考虑下面的问题:
欧拉函数公式 求欧拉函数
直接计算是
判断两个数是否互质,首先分解质因数
那么就要求对于任意
全集大小
因此可得
这就是欧拉函数的数学表示啦
容斥原理一般化 容斥原理常用于集合的计数问题,而对于两个集合的函数
那么就有
证明 接下来我们简单证明一下。我们从等式的右边开始推:
我们发现后半部分的求和与
记关于集合
因此原来的式子的值是
分析发现,仅当
综上所述,得证。
推论 该形式还有这样一个推论。在全集
那么
这个推论其实就是补集形式,证法类似。
DAG 计数 DAG 计数 对
直接 DP 考虑 DP,定义
计算上式的复杂度是
放宽限制 上述 DP 的定义是恰好
计算上式的复杂度是
Min-max 容斥 对于满足 全序 关系并且其中元素满足可加减性的序列
证明: 考虑做一个到一般容斥原理的映射。对于
那么容易发现,对于
然后再把
证毕
但是你可能觉得这个式子非常蠢,最大值明明可以直接求。之所以 min-max 容斥这么重要,是因为它在期望上也是成立的,即:
证明: 我们考虑计算期望的一种方法:
其中
我们对后面的
调换求和顺序:
证毕
还有更强的:
规定若
证明: 不妨设
又因为有组合恒等式:
当
否则:
所以:
剩下三个是类似的。
证毕
根据 min-max 容斥,我们还可以得到下面的式子:
因为
PKUWC2018 随机游走 PKUWC2018 随机游走 给定一棵
有
特别地,点
对
期望游走的步数也就是游走的时间。那么设随机变量
使用 min-max 容斥可以得到
对于一个集合
考虑
如果直接高斯消元,复杂度
不妨设根结点是
对于非叶结点
那么变换一下可以得到
于是我们把
解一下这个方程我们就得到了
这样,我们可以对于每一个
回到容斥的部分,我们知道
不妨设
习题 参考文献 王迪《容斥原理》,2013 年信息学奥林匹克中国国家队候选队员论文集
Cyhlnj《有标号的 DAG 计数系列问题》
Wikipedia - 全序关系
2024/4/29 08:59:48 ,更新历史 在 GitHub 上编辑此页! CCXXXI , ComeIntoCalm , dkz051 , Enter-tainer , Great-designer , hsfzLZH1 , iamtwz , Ir1d , Jiangkangping , kenlig , lychees , megakite , MegaOwIer , ouuan , Peanut-Tang , sbofgayschool , ShizuhaAki , sshwy , StableAgOH , tder6 , Tiphereth-A , Xeonacid CC BY-SA 4.0 和 SATA