Stoer–Wagner 算法
定义
由于取消了 源汇点 的定义,我们需要对 割 的概念进行重定义。
(其实是网络流部分有关割的定义与维基百科不符,只是由于一般接触到的割都是「有源汇的最小割问题」,因此这个概念也就约定俗成了。)
割
去掉其中所有边能使一张网络流图不再连通(即分成两个子图)的边集称为图的割。
即:在无向图  中,设
中,设  为图
为图  中一些弧的集合,若从
中一些弧的集合,若从  中删去
中删去  中的所有弧能使图
中的所有弧能使图  不是连通图,称
不是连通图,称  图
图  的一个割。
的一个割。
有源汇点的最小割问题
同 最小割 中的定义。
无源汇点的最小割问题
包含的弧的权和最小的割。也称为全局最小割。
显然,直接跑网络流的复杂度是行不通的。
Stoer–Wagner 算法
引入
Stoer–Wagner 算法在 1995 年由Mechthild Stoer与Frank Wagner提出,是一种通过 递归 的方式来解决 无向正权图 上的全局最小割问题的算法。
性质
算法复杂度  一般可近似看作
一般可近似看作  。
。
它的实现基于以下基本事实:设图  中有任意两点
中有任意两点  。那么任意一个图
。那么任意一个图  的割
的割  ,或者有
,或者有  在同一连通块中,或者有
在同一连通块中,或者有  是一个
是一个  割。
割。
过程
- 在图
 中任意指定两点
中任意指定两点  ,并且以这两点作为源汇点求出图
,并且以这两点作为源汇点求出图  的
的  最小割(定义为cut of phase),更新当前答案。
最小割(定义为cut of phase),更新当前答案。 - 「合并」点
 ,如果图
,如果图  中
中  大于
大于  ,则回到第一步。
,则回到第一步。 - 输出所有cut of phase的最小值。
合并两点  :删除
:删除  之间的连边
之间的连边  ,对于
,对于  中任意一点
中任意一点  ,删除
,删除  ,并将其边权
,并将其边权  加到
加到  上
上
解释:如果  在同一连通块,对于
在同一连通块,对于  中的一点
中的一点  ,假如
,假如  ,那么
,那么  也一定成立,否则因为
也一定成立,否则因为  连通,
连通, 连通,导致
连通,导致  在同一连通块,此时
在同一连通块,此时  将比
将比  更优。反之亦然。所以
更优。反之亦然。所以  可以看作同一点。
可以看作同一点。
步骤 1 考虑了  不在同一连通块的情形,步骤 2 考虑了剩余的情况。由于每次执行步骤 2 都会使
不在同一连通块的情形,步骤 2 考虑了剩余的情况。由于每次执行步骤 2 都会使  减小
减小  ,因此算法将在进行
,因此算法将在进行  后结束。
后结束。
S-T 最小割的求法
(显然不是网络流。)
假设进行若干次合并以后,当前图  ,执行步骤 1。
,执行步骤 1。
我们构造一个集合  ,初始时令
,初始时令  。
。
我们每次将  中所有点中,满足
中所有点中,满足  ,且权值函数
,且权值函数  最大的节点加入集合
最大的节点加入集合  ,直到
,直到  。
。
其中权值函数的定义:

(若  ,则
,则  )。
)。
容易知道所有点加入  的顺序是固定的,令
的顺序是固定的,令  表示第
表示第  个加入
个加入  的点,
的点, ;
; 表示
表示  被加入
被加入  后
后  的大小,即
的大小,即  被加入的顺序。
被加入的顺序。
则对任意点  ,一个
,一个  到
到  的割即为
的割即为  。
。
证明
定义一个点  被激活,当且仅当
被激活,当且仅当  在加入
在加入  中时,发现在
中时,发现在  此时最后一个点
此时最后一个点  早于
早于  加入集合,并且在图
加入集合,并且在图  中,
中, 与
与  不在同一连通块。
不在同一连通块。
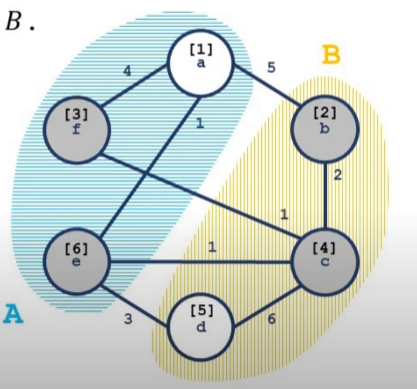
如图,蓝色区域和黄色区域为两个不同的连通块,方括号中的数字为加入  的顺序。灰色节点为活跃节点,白色节点则不是活跃节点。
的顺序。灰色节点为活跃节点,白色节点则不是活跃节点。
定义  ,也就是严格早于
,也就是严格早于  加入
加入  的点,令
的点,令  为
为  的诱导子图(点集为
的诱导子图(点集为  )的边集。(注意包含点
)的边集。(注意包含点  。)
。)
定义诱导割  为
为  。
。 。
。
Lemma 1
对于任何被激活的点  ,
, 。
。
证明:使用数学归纳法。
对于第一个被激活的点  ,由定义可知
,由定义可知  。
。
对于之后两个被激活的点  ,假设
,假设  ,则有:
,则有:

又,已知:
 并且
并且  联立可得:
联立可得:

由于  对
对  有贡献而对
有贡献而对  没有贡献,在所有边均为正权的情况下,可导出:
没有贡献,在所有边均为正权的情况下,可导出:

由归纳法得证。
由于  ,并且
,并且  不在同一连通块,因此
不在同一连通块,因此  会被激活,由此可以得出
会被激活,由此可以得出  。
。
P5632【模板】Stoer–Wagner 算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 | #include <bits/stdc++.h>
using namespace std;
const int N = 601;
int fa[N], siz[N], edge[N][N];
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
int dist[N], vis[N], bin[N];
int n, m;
int contract(int &s, int &t) { // Find s,t
memset(dist, 0, sizeof(dist));
memset(vis, false, sizeof(vis));
int i, j, k, mincut, maxc;
for (i = 1; i <= n; i++) {
k = -1;
maxc = -1;
for (j = 1; j <= n; j++)
if (!bin[j] && !vis[j] && dist[j] > maxc) {
k = j;
maxc = dist[j];
}
if (k == -1) return mincut;
s = t;
t = k;
mincut = maxc;
vis[k] = true;
for (j = 1; j <= n; j++)
if (!bin[j] && !vis[j]) dist[j] += edge[k][j];
}
return mincut;
}
const int inf = 0x3f3f3f3f;
int Stoer_Wagner() {
int mincut, i, j, s, t, ans;
for (mincut = inf, i = 1; i < n; i++) {
ans = contract(s, t);
bin[t] = true;
if (mincut > ans) mincut = ans;
if (mincut == 0) return 0;
for (j = 1; j <= n; j++)
if (!bin[j]) edge[s][j] = (edge[j][s] += edge[j][t]);
}
return mincut;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
if (m < n - 1) {
cout << 0;
return 0;
}
for (int i = 1; i <= n; ++i) fa[i] = i, siz[i] = 1;
for (int i = 1, u, v, w; i <= m; ++i) {
cin >> u >> v >> w;
int fu = find(u), fv = find(v);
if (fu != fv) {
if (siz[fu] > siz[fv]) swap(fu, fv);
fa[fu] = fv, siz[fv] += siz[fu];
}
edge[u][v] += w, edge[v][u] += w;
}
int fr = find(1);
if (siz[fr] != n) {
cout << 0;
return 0;
}
cout << Stoer_Wagner();
return 0;
}
|
复杂度分析与优化
contract操作的复杂度为  。
。
一共进行  次contract,总复杂度为
次contract,总复杂度为  。
。
根据 最短路 的经验,算法瓶颈在于找到权值最大的点。
在一次contract中需要找  次堆顶,并递增地修改
次堆顶,并递增地修改  次权值。
次权值。
斐波那契堆 可以胜任  查找堆顶和
查找堆顶和  递增修改权值的工作,理论复杂度可以达到
递增修改权值的工作,理论复杂度可以达到  ,但是由于斐波那契堆常数过大,码量高,实际应用价值偏低。
,但是由于斐波那契堆常数过大,码量高,实际应用价值偏低。
(实际测试中开 O2 还要卡评测波动才能过。)
本页面最近更新:2024/5/2 00:08:23,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:DanJoshua, opsiff, yingqi-z20, yzy-1, CroMarmot, Enter-tainer, EntropyIncreaser, iamtwz, ImpleLee, kenlig, Marcythm, Menci, sldpzshdwz, Tiphereth-A
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用
