基数排序 提醒 本页面要介绍的不是 计数排序
本页面将简要介绍基数排序。
定义 基数排序(英语:Radix sort)是一种非比较型的排序算法,最早用于解决卡片排序的问题。基数排序将待排序的元素拆分为
如果是从第
如果是从第
k - 关键字元素的比较 下面用
假如元素有
比较两个元素的第 比较两个元素的第 …… 比较两个元素的第 例子:
如果对自然数进行比较,将自然数按个位对齐后往高位补齐 如果对字符串基于字典序进行比较,一个字符串从左往右数第 C++ 自带的 std::pair 与 std::tuple 的默认比较方法与上述的相同。 MSD 基数排序 基于 k - 关键字元素的比较方法,可以想到:先比较所有元素的第 具有相同第 ,再比较它们的第
由于是从第
算法流程 将待排序的元素拆分为 具有相同关键字的元素 再对第 具有相同关键字的元素 再对第
一般而言,我们默认基数排序是稳定的,所以在 MSD 基数排序中,我们也仅仅考虑借助 稳定算法 (通常使用计数排序)完成内层对关键字的排序。
正确性参考上文 k - 关键字元素的比较。
参考代码 对自然数排序 下面是使用迭代式 MSD 基数排序对 unsigned int 范围内元素进行排序的 C++ 参考代码,可调整
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 #include <algorithm>
#include <stack>
#include <tuple>
#include <vector>
using std :: copy ; // from <algorithm>
using std :: make_tuple ;
using std :: stack ;
using std :: tie ;
using std :: tuple ;
using std :: vector ;
typedef unsigned int u32 ;
typedef unsigned int * u32ptr ;
void MSD_radix_sort ( u32ptr first , u32ptr last ) {
const size_t maxW = 0x100000000llu ;
const u32 maxlogW = 32 ; // = log_2 W
const u32 W = 256 ; // 计数排序的值域
const u32 logW = 8 ;
const u32 mask = W - 1 ; // 用位运算替代取模,详见下面的 key 函数
u32ptr tmp =
( u32ptr ) calloc ( last - first , sizeof ( u32 )); // 计数排序用的输出空间
typedef tuple < u32ptr , u32ptr , u32 > node ;
stack < node , vector < node >> s ;
s . push ( make_tuple ( first , last , maxlogW - logW ));
while ( ! s . empty ()) {
u32ptr begin , end ;
size_t shift , length ;
tie ( begin , end , shift ) = s . top ();
length = end - begin ;
s . pop ();
if ( begin + 1 >= end ) continue ; // elements <= 1
// 计数排序
u32 cnt [ W ] = {};
auto key = []( const u32 x , const u32 shift ) { return ( x >> shift ) & mask ; };
for ( u32ptr it = begin ; it != end ; ++ it ) ++ cnt [ key ( * it , shift )];
for ( u32 value = 1 ; value < W ; ++ value ) cnt [ value ] += cnt [ value - 1 ];
// 求完前缀和后,计算相同关键字的元素范围
if ( shift >= logW ) {
s . push ( make_tuple ( begin , begin + cnt [ 0 ], shift - logW ));
for ( u32 value = 1 ; value < W ; ++ value )
s . push ( make_tuple ( begin + cnt [ value - 1 ], begin + cnt [ value ],
shift - logW ));
}
u32ptr it = end ;
do {
-- it ;
-- cnt [ key ( * it , shift )];
tmp [ cnt [ key ( * it , shift )]] = * it ;
} while ( it != begin );
copy ( tmp , tmp + length , begin );
}
}
对字符串排序 下面是使用迭代式 MSD 基数排序对 空终止字节字符串 基于字典序进行排序的 C++ 参考代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 #include <algorithm>
#include <stack>
#include <tuple>
#include <vector>
using std :: copy ; // from <algorithm>
using std :: make_tuple ;
using std :: stack ;
using std :: tie ;
using std :: tuple ;
using std :: vector ;
typedef char * NTBS ; // 空终止字节字符串
typedef NTBS * NTBSptr ;
void MSD_radix_sort ( NTBSptr first , NTBSptr last ) {
const size_t W = 128 ;
const size_t logW = 7 ;
const size_t mask = W - 1 ;
NTBSptr tmp = ( NTBSptr ) calloc ( last - first , sizeof ( NTBS ));
typedef tuple < NTBSptr , NTBSptr , size_t > node ;
stack < node , vector < node >> s ;
s . push ( make_tuple ( first , last , 0 ));
while ( ! s . empty ()) {
NTBSptr begin , end ;
size_t index , length ;
tie ( begin , end , index ) = s . top ();
length = end - begin ;
s . pop ();
if ( begin + 1 >= end ) continue ; // elements <= 1
// 计数排序
size_t cnt [ W ] = {};
auto key = []( const NTBS str , const size_t index ) { return str [ index ]; };
for ( NTBSptr it = begin ; it != end ; ++ it ) ++ cnt [ key ( * it , index )];
for ( char ch = 1 ; value < W ; ++ value ) cnt [ ch ] += cnt [ ch - 1 ];
// 求完前缀和后,计算相同关键字的元素范围
// 对于 NTBS,如果此刻末尾的字符是 \0 则说明这两个字符串相等,不必继续迭代
for ( char ch = 1 ; ch < W ; ++ ch )
s . push ( make_tuple ( begin + cnt [ ch - 1 ], begin + cnt [ ch ], index + 1 ));
NTBSptr it = end ;
do {
-- it ;
-- cnt [ key ( * it , index )];
tmp [ cnt [ key ( * it , index )]] = * it ;
} while ( it != begin );
copy ( tmp , tmp + length , begin );
}
free ( tmp );
}
由于两个字符串的比较很容易冲上
与桶排序的关系 前置知识:桶排序
桶排序需要其它的排序算法来完成对每个桶内部元素的排序。但实际上,完全可以对每个桶继续执行桶排序,直至某一步桶的元素数量
因此 MSD 基数排序的另一种理解方式是:使用桶排序实现的桶排序。
也因此,可以提出 MSD 基数排序在时间常数上的一种优化方法:假如到某一步桶的元素数量
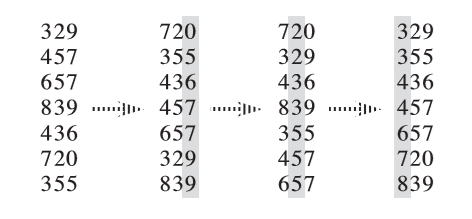
LSD 基数排序 MSD 基数排序从第
而将递归的操作反过来:从第
算法流程 将待排序的元素拆分为 所有元素 的第 所有元素 的第 所有元素 的第 所有元素 的第
LSD 基数排序也需要借助一种 稳定算法 完成内层对关键字的排序。同样的,通常使用计数排序来完成。
LSD 基数排序的正确性可以参考 《算法导论(第三版)》第 8.3-3 题的解法 或参考下面的解释:
正确性 回顾一下 k - 关键字元素的比较方法,
假如想通过 而想通过 …… 而想通过 现在,将顺序反过来:
而知道通过比较 …… 而知道通过比较 而知道通过比较 在这个过程中,对每个关键字边比较边重排元素的顺序,就得到了 LSD 基数排序。
伪代码 参考代码 下面是使用 LSD 基数排序实现的对 k - 关键字元素的排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 const int N = 100010 ;
const int W = 100010 ;
const int K = 100 ;
int n , w [ K ], k , cnt [ W ];
struct Element {
int key [ K ];
bool operator < ( const Element & y ) const {
// 两个元素的比较流程
for ( int i = 1 ; i <= k ; ++ i ) {
if ( key [ i ] == y . key [ i ]) continue ;
return key [ i ] < y . key [ i ];
}
return false ;
}
} a [ N ], b [ N ];
void counting_sort ( int p ) {
memset ( cnt , 0 , sizeof ( cnt ));
for ( int i = 1 ; i <= n ; ++ i ) ++ cnt [ a [ i ]. key [ p ]];
for ( int i = 1 ; i <= w [ p ]; ++ i ) cnt [ i ] += cnt [ i - 1 ];
// 为保证排序的稳定性,此处循环i应从n到1
// 即当两元素关键字的值相同时,原先排在后面的元素在排序后仍应排在后面
for ( int i = n ; i >= 1 ; -- i ) b [ cnt [ a [ i ]. key [ p ]] -- ] = a [ i ];
memcpy ( a , b , sizeof ( a ));
}
void radix_sort () {
for ( int i = k ; i >= 1 ; -- i ) {
// 借助计数排序完成对关键字的排序
counting_sort ( i );
}
}
实际上并非必须从后往前枚举才是稳定排序,只需对 cnt 数组进行等价于 std::exclusive_scan 的操作即可。
例题 洛谷 P1177【模板】快速排序 给出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 #include <algorithm>
#include <iostream>
#include <utility>
void radix_sort ( int n , int a []) {
int * b = new int [ n ]; // 临时空间
int * cnt = new int [ 1 << 8 ];
int mask = ( 1 << 8 ) - 1 ;
int * x = a , * y = b ;
for ( int i = 0 ; i < 32 ; i += 8 ) {
for ( int j = 0 ; j != ( 1 << 8 ); ++ j ) cnt [ j ] = 0 ;
for ( int j = 0 ; j != n ; ++ j ) ++ cnt [ x [ j ] >> i & mask ];
for ( int sum = 0 , j = 0 ; j != ( 1 << 8 ); ++ j ) {
// 等价于 std::exclusive_scan(cnt, cnt + (1 << 8), cnt, 0);
sum += cnt [ j ], cnt [ j ] = sum - cnt [ j ];
}
for ( int j = 0 ; j != n ; ++ j ) y [ cnt [ x [ j ] >> i & mask ] ++ ] = x [ j ];
std :: swap ( x , y );
}
delete [] cnt ;
delete [] b ;
}
int main () {
std :: ios :: sync_with_stdio ( false );
std :: cin . tie ( 0 );
int n ;
std :: cin >> n ;
int * a = new int [ n ];
for ( int i = 0 ; i < n ; ++ i ) std :: cin >> a [ i ];
radix_sort ( n , a );
for ( int i = 0 ; i < n ; ++ i ) std :: cout << a [ i ] << ' ' ;
delete [] a ;
return 0 ;
}
性质 稳定性 如果对内层关键字的排序是稳定的,则 MSD 基数排序和 LSD 基数排序都是稳定的排序算法。
时间复杂度 通常而言,基数排序比基于比较的排序算法(比如快速排序)要快。但由于需要额外的内存空间,因此当内存空间稀缺时,原地置换算法(比如快速排序)或许是个更好的选择。
一般来说,如果每个关键字的值域都不大,就可以使用 计数排序 作为内层排序,此时的复杂度为
空间复杂度 MSD 基数排序和 LSD 基数排序的空间复杂度都为
参考资料与注释 2023/10/14 17:35:11 ,更新历史 在 GitHub 上编辑此页! NachtgeistW , Alisahhh , countercurrent-time , Early0v0 , Enter-tainer , H-J-Granger , hly1204 , iamtwz , Ir1d , Konano , ksyx , OhGaGaGaGa , ouuan , partychicken , sbofgayschool , SukkaW , Tiphereth-A , untitledunrevised CC BY-SA 4.0 和 SATA